RESEARCH METHOD

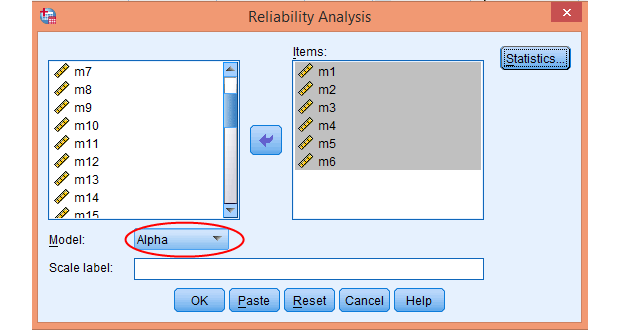
Minh họa thực hiện phân tích phân tách DA trên Stata Hàm phân tách tuyến tính, chẳng hạn phân tích phân tách (discriminant analysis) được sử dụng để thực hiện một kiểm định đa biến về sự khác nhau...

Hướng dẫn giải thích và đọc kết quả phân tích EFA trên Stata Tiếp tục bài giới thiệu về nhân tố khám phá EFA, bài viết này sẽ minh họa các bước thực hiện và giải thích các kết quả phân tích nhân t...

Phân tích hệ số tin cậy Cronbach alpha trên Stata Hệ số tin cậy Cronbach anpha được sử dụng để kiểm tra độ tin cậy bên trong của thang đo. Nó cho biết mức độ tương quan giữa các biến trong mỗi nh...

Hướng dẫn thực hiện phân tích nhân tố khám phá EFA trên Stata Phân tích nhân tố khám phá EFA (Exploratory factor analysis) là một phương pháp rút gọn dữ liệu, cho biết mối quan hệ giữa các nhóm bi...

Giới thiệu phép xoay nhân tố trong phân tích EFA Một trong các bước quan trọng của phân tích nhân tố khám phá cũng như phân tích thành phần chính (PCA) là lựa chọn một phép xoay nhân tố hoặc thàn...

Phân biệt PCA và EFA trong phân tích nhân tố Phân tích thành phần chính (PCA) và phân tích nhân tố khám phá (EFA) là 2 phương pháp được sử dụng phổ biến trong các nghiên cứu thị trường. Cả hai ph...

Hướng dẫn đọc kết quả phân tích CATPCA trên SPSS Phân tích CATPCA hay còn gọi là phân tích thành phần chính dạng danh mục CATPCA (Categorical principal components analysis) là được sử dụng tinh g...

Hướng dẫn thực hiện phân tích CATPCA trên SPSS Phân tích CATPCA hay còn gọi là phân tích thành phần chính dạng danh mục CATPCA (Categorical principal components analysis) là được sử dụng tinh giả...

Hướng dẫn thục hiện phương pháp phân tách Stepwise trên SPSS Phương pháp phân tách stepwise (Stepwise Discriminant Analysis) có ý nghĩa tương đồng với phân tích hồi quy đa biến stepwise ở chổ là ...

Hướng dẫn đọc kết quả phân tích phân tách DA trên SPSS Trong phương pháp phân tách chúng ta cố gắng phân nhóm dựa vào sự tách biệt trong mỗi đối tượng. Vì vậy, đầu tiên chúng ta cần xem liệu có s...

Minh họa thực hiện phương pháp phân tách DA trên SPSS Phương pháp phân tách sử dụng một tập hợp các biến độc lập dạng liên tục (khoảng, tỉ lệ) để giải thích cho một biến phụ thuộc dạng phân loại....

Phương pháp phân tách (Discriminant analysis) là một phương pháp phân tích thống kê được dùng rất nhiều trong Data mining để phân loại các đối tượng (object) vào các nhóm dựa việc đo lường các đặc trư...

Tiếp tục bài viết phân tích cluster thứ bậc qua phương pháp Ward, và phân tích cluster không thứ bậc theo phương pháp K-Means, bài viết này sẽ trình bày một phương pháp khác có tính ưu việt hơn so với...

Ngược lại với phân tích cluster thứ bậc, phương pháp phân tích cluster không thứ bậc (Non Hierarchical Cluster Analysis) không bao gồm quy trình phân nhóm hình cây mà thay vào đó là phân bổ các đối tư...

Phân tích cluster được ứng dụng trong rất nhiều lĩnh vực từ vi mô như nghiên cứu hành vi xã hội, tâm lý, địa lý, kinh doanh… đến nghiên cứu vĩ mô ở cấp độ đầu tư của ngành chẳng hạn. Trong nghiên cứu ...

Để chuyển dữ liệu thành thông tin, thành kiến thức thì chúng ta phải biết đơn giản hóa dữ liệu. Có 2 cách phổ biến để đơn giản hóa dữ liệu, đó là phân tích nhân tố (factor analysis) và phân tích clust...

Hệ số Cronbach anpha là một hệ số kiểm định thống kê về mức độ tin cậy và tương quan trong giữa các biến quan sát trong thang đo. Tư tưởng chung của phương pháp này là tìm kiếm sự vô lý nếu có trong c...

Phân tích nhân tố khám phá (EFA) là một trong những phương pháp phân tích thống kê dùng để rút gọn một tập hợp nhiều biến quan sát phụ thuộc lẫn nhau thành một tập biến ít hơn để chúng có ý nghĩa hơn ...

Minh họa thực hiện ước lượng mô hình PTR trên Stata Các mô hình ngưỡng được sử dụng rộng rãi trong kinh tế vĩ mô và phân tích tài chính để giải thích các mối quan hệ phi tuyến giữa các biến. Bên ...

Giới thiệu mô hình hồi quy ngưỡng – PTR Các mô hình ngưỡng (threshold models) được sử dụng rộng rãi trong các phân tích tài chính, vĩ mô bởi sự đơn giản và rõ ràng trong hàm ý ...

Minh họa thực hiện ước lượng FMOLS, DOLS trên EViews Tùy theo đặc điểm của dữ liệu, mô hình nghiên cứu mà các bạn có thể lựa chọn phương thức ước lượng phù hợp giữa Pooled, Pooled (weighted), Gro...

Tổng hợp các kiểm định dữ liệu bảng trên EViews Kiểm định sự tồn tại của các tác động riêng rẽ của các đối tượng hoặc các thời điểm trong ước lượng dữ liệu bảng là một trong những kiểm định quan ...

Hướng dẫn thiết lập ước lượng FMOLS, DOLS trên EViews Sự lựa chọn giữa FMOLS và DOLS dựa trên cơ sở về tính đồng nhất của các hệ số phương sai dài hạn. Nếu các hệ số này là đồng nhất giữa các đơn...

Hướng dẫn kiểm tra đồng kết hợp dữ liệu bảng trên EViews Nếu 2 chuỗi thời gian, X và Y, là đồng kết hợp thì phải tồn tại một mối quan hệ nhân quả Granger từ X đến Y hoặc từ Y đến X hoặc theo cả 2...

Minh họa thực hiện ước lượng PMG trên EViews Mô hình ARDL có thể xảy ra vấn đề thiên chệch khi có sự tương quan giữa biến giải thích sai phân trung bình với thành phần sai số. Sự thiên chệch này ...

Phân tích thành phần chính PCA trên EViews Về mặt nguyên tắc thực hiện, phân tích thành phần chính PCA sẽ mô hình hóa cấu trúc phương sai của một tập biến quan sát bằng cách sử dụng kết hợp tuyến...

Vấn đề hiệp phương sai đồng thời trong dữ liệu bảng Hiệp phương sai đồng thời (contemporaneous covariances) trong dữ liệu bảng được sử dụng rộng rãi trong phân tích dữ liệu bảng. Thông qua mối tư...

Hướng dẫn thực hiện Breakpoint Unit Test trên EViews Perron (1989) đã chỉ ra rằng các kiểm định nghiệm đơn vị thông thường sẽ bị chệch về hướng bác bỏ giả thiết H0 khi dữ liệu là dừng xu thế với ...

Hướng dẫn thực hiện kiểm định nghiệm đơn vị bảng trên EViews Kiểm định nghiệm đơn vị là để phân biệt giữa tính xu thế và tính dừng của dữ liệu. Kiểm định nghiệm đơn vị với dữ liệu bảng có hiệu q...

Minh họa thực hiện kiểm định nhân quả dữ liệu bảng trên EViews Theo Hurlin và Venet (2001) kiểm định nhân quả với dữ liệu bảng sẽ hiệu quả hơn so với nhân quả Granger trong dữ liệu chuỗi thời gia...

Hướng dẫn thực hiện lựa chọn mô hình FE, RE trên EViews Bài viết minh họa cách lựa chọn phương pháp ước lượng dữ liệu bảng giữa OLS, FE, RE trên EViews. Cụ thể là kiểm định sự tồn tại của các ảnh...

Minh họa thực hành ước lượng dữ liệu bảng trên EViews Bài viết sau sẽ minh họa cách thực hành ước lượng dữ liệu bảng trên Eviews từ bước nhập dữ liệu, khai báo dữ liệu, ước lượng mô hình dữ liệu ...

Ước lượng dữ liệu bảng trên EViews với câu lệnh LS Cú pháp của lệnh hồi quy theo phương pháp bình phương bé nhất (tuyến tính lẫn phi tuyến) như sau: ls(options) y x1 x2… hay tổng quát là ls(opti...

Thực hiện ước lượng GMM trên EViews với câu lệnh GMM Cú pháp câu lệnh gmm để ước lượng theo phương pháp GMM như sau: gmm(options) y x1 @ z1 gmm(options) specification @ z1 Diễn giải câu lệnh: ...

Giới thiệu phương pháp PMG trong dữ liệu bảng Phương pháp GMM được sử dụng để khắc phục sự tương quan giữa các biến giải thích với các thành phần sai số (μi hoặc εit) bằng cách sử dụng các biến đ...

Xử lí vấn đề biến nội sinh bằng phương pháp GMM Các phương pháp ước lượng dữ liệu bảng như Fixed effect (FE, FD, LSDV) hoặc Random effects được sử dụng chủ yếu để ước lượng các mô hình dữ liệu bản...

Phân biệt phương pháp S-GMM và D-GMM Các phương pháp ước lượng dữ liệu bảng như Fixed effect (FE, FD, LSDV) hoặc Random effects được sử dụng chủ yếu để ước lượng các mô hình dữ liệu bảng tĩnh tuyế...

Phương pháp D-GMM và S-GMM thường được sử dụng để ước lượng các dữ liệu bảng động (có biến trễ), các dữ liệu bảng có N lớn T nhỏ hoặc tồn tại các vấn đề liên quan đến biến nội sinh, phương sai thay đổ...

GMM là gì? GMM được sử dụng khi nào? Trong các mô hình dữ liệu bảng động tuyến tính, khi T nhỏ thì các phương pháp ước lượng tác động cố định FE hoặc phương pháp sai phân bậc 1 là không phù hợp (...

Kiểm định Hausman, khi nào sử dụng? Theo cách tiếp cận truyền thống thì dữ liệu bảng có thể được ước lượng thông qua 2 mô hình tác động cố định (FEM) và tác động ngẫu nhiên (REM), đồng thời sử dụ...

Yếu tố không quan sát được, không thay đổi theo thời gian Unobserved time-invariant hay Unobserved time-constant là một thuật ngữ thể hiện yếu tố không thay đổi theo thời gian không quan sát được. ...

Một cách nhìn khác về mô hình FE, RE Dữ liệu đa bậc tổng hợp dữ liệu nhiều lớp, do vậy, chứa đựng rất nhiều thông tin. Tuy nhiên các mô hình ước lượng như OLS, OLS với robust hoặc cluster robust ...

Lựa chọn mô hình RE với FE Bên cạnh ước lượng thô OLS, để ước lượng dữ liệu bảng chúng ta lần lượt đã tìm hiểu qua 2 mô hình khác đó là mô hình tác động cố định (FE) và mô hình tác động ngẫu nhiê...

Giới thiệu mô hình tác động ngẫu nhiên Bên cạnh mô hình tác động cố định, mô hình tác động ngẫu nhiên (Random Effect) là một trong hai mô hình được sử dụng phổ biến trong ước lượng các dữ liệu bả...

Giới thiệu mô hình tác động cố định Mô hình tác động cố định (Fixed Effect) là một trong hai mô hình phổ biến được sử dụng trong ước lượng dữ liệu bảng. Bài viết này sẽ đi sâu trình bày phương ph...

Giới thiệu Ưu & Nhược điểm của dữ liệu bảng Dữ liệu bảng đôi khi còn được gọi là dữ liệu dài (longitudinal data). Dữ liệu bảng là sự kết hợp của dữ liệu chéo (cross-section) và dữ liệu thời g...

Phân biệt mô hình hồi quy logit và hồi quy probit Khi một biến phụ thuộc là biến danh mục (nhị phân, thứ tự hoặc định danh) thì phương pháp bình phương tối thiểu OLS sẽ không còn là một ước lượng...

Minh họa thực hiện hồi quy probit trên Stata Hồi quy Probit, đôi khi còn được gọi là mô hình probit, được sử dụng để ước lượng mô hình có biến phụ thuộc dạng nhị phân. Trong hồi quy probit, nghịc...

Minh họa thực hiện hồi quy tobit trên Stata Mô hình tobit, đôi khi còn được gọi là mô hình hồi quy kiểm duyệt (censored regression model), được xây dựng để ước lượng mối quan hệ tuyến tính giữa c...

Minh họa thực hiện hồi quy khoảng trên Stata Hồi quy khoảng (Interval Regression) được sử dụng để ước lượng mô hình có các biến phụ thuộc bị kiểm duyệt. Dữ liệu bị kiểm duyệt trong hồi quy khoảng...