Mô hình tác động đồng thời SEM
Từ khóa: hệ phương trình đồng thời, mô hình SEM, phương trình cấu trúc, phương trình thu gọn, tính đồng thời, tác động phản hồi, biến nội sinh, hồi quy gián tiếp, hồi quy hai giai đoạn, ước lượng IV, Simultaneous Equations Models, structural equations, reduced form equations, edogeneity, 2SLS, ILS.
1. Giới thiệu về mô hình tác động đồng thời SEM
Bên cạnh hai vấn đề phổ biến liên quan đến tính nội sinh (endogeneity) của mô hình là bỏ sót biến, sai số trong biến đo lường thì vấn đề về tính đồng thời của biến (Simultaneity) cũng rất được quan tâm. Tính đồng thời của biến thường được phát hiện trong các mô hình về điểm cân bằng thị trường, mô hình tác động tương hỗ giữa các yếu tố (số lượng cảnh sát và tỉ lệ tội phạm, chẳng hạn). Bài toán liên quan đến mô hình này còn được gọi là hệ phương trình đồng thời SEMs (Simultaneous Equations Models). Hệ phương trình đồng thời là tập hợp nhiều biểu thức riêng rẻ, mà mỗi biểu thức được gọi là các phương trình cấu trúc (structural equations). Các phương trình cấu trúc này bao gồm một biến nội sinh (endogenous variable) và nhiều biến ngoại sinh (exogenous variables). Các hệ số ước lượng của các biến trong mỗi phương trình cấu trúc được gọi là các thông số cấu trúc (structural parameters). Ở đây, mỗi biến nội sinh của các phương trình cấu trúc được xác định đồng thời qua các phương trình cấu trúc khác. Do vậy, trong trường hợp này, kỹ thuật hồi quy OLS sẽ không phù hợp cho việc ước lượng hệ phương trình đồng thời này.
2. Phương pháp ước lượng mô hình
Bên cạnh hai vấn đề phổ biến liên quan đến tính nội sinh (endogeneity) của mô hình là bỏ sót biến, sai số trong biến đo lường thì vấn đề về tính đồng thời của biến (Simultaneity) cũng rất được quan tâm. Tính đồng thời của biến thường được phát hiện trong các mô hình về điểm cân bằng thị trường, mô hình tác động tương hỗ giữa các yếu tố (số lượng cảnh sát và tỉ lệ tội phạm, chẳng hạn). Bài toán liên quan đến mô hình này còn được gọi là hệ phương trình đồng thời SEMs (Simultaneous Equations Models). Hệ phương trình đồng thời là tập hợp nhiều biểu thức riêng rẻ, mà mỗi biểu thức được gọi là các phương trình cấu trúc (structural equations). Các phương trình cấu trúc này bao gồm một biến nội sinh (endogenous variable) và nhiều biến ngoại sinh (exogenous variables). Các hệ số ước lượng của các biến trong mỗi phương trình cấu trúc được gọi là các thông số cấu trúc (structural parameters). Ở đây, mỗi biến nội sinh của các phương trình cấu trúc được xác định đồng thời qua các phương trình cấu trúc khác. Do vậy, trong trường hợp này, kỹ thuật hồi quy OLS sẽ không phù hợp cho việc ước lượng hệ phương trình đồng thời này.
 |
| Ước lượng mô hình SEM trên Stata: https://vietlod.com/mo-hinh-sems-stata |
2. Phương pháp ước lượng mô hình
Có 3 các để ước lượng hệ phương trình đồng thời này: (i) bình phương tối thiểu gián tiếp (ILS); (ii) ước lượng IV thông qua biến công cụ z; (iii) ước lượng hai giai đoạn tối thiểu (2SLS). Tùy vào điều kiện nhận dạng mô hình (hệ phương trình) mà người phân tích áp dụng phương pháp thích hợp. ILS với ước lượng OLS cho các phương trình thu gọn (Reduced form equations) sẽ được sử dụng khi mô hình SEMs được nhận dạng chính xác (exact identified). Ước lượng IV được sử dụng khi có một biến công cụ phù hợp làm công cụ (instrumented) cho biến nội sinh. Cuối cùng, 2SLS sẽ được sử dụng khi mô hình SEMs được nhận dạng chính xác hoặc nhận dạng quá mức (over identified).
Nhắc lại: phương trình thu gọn là phương trình biễu diễn của biến nội sinh theo các biến ngoại sinh và thành phần sai số của phương trình cấu trúc. Phương trình cấu trúc được xác định thông qua phương trình thu gọn (xác định hệ số của phương trình thu gọn, từ đó, xác định các hệ số của phương trình cấu trúc).
Giả sử gọi G là số phương trình cấu trúc có trong hệ phương trình SEMs. So sánh (hạng ma trận của SEMs) số biến loại ra khỏi phương trình cấu trúc (kí hiệu là N) với G – 1 sẽ dẫn đến các vấn đề như (i) nhận dạng quá mức (N lớn hơn G – 1); (ii) nhận dạng chính xác (N = G – 1); (iii) không nhận dạng được (N nhỏ hơn G – 1).
3. Ví dụ minh họa
Giả sử, ước lượng mô hình tham gia lao động của các phụ nữ đã lập gia đình. Hệ phương trình SEMs có dạng như sau:
 |
| Mô hình SEM về tham gia lao động cả các phụ nữ đã lập gia đình |
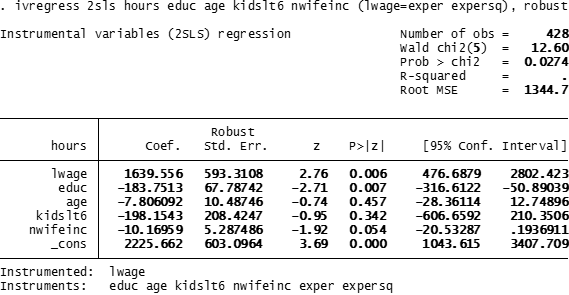 |
| Ước lượng 2SLS cho hours trong mô hình SEM |
 |
| Ước lượng 2SLS cho lwage trong mô hình SEM |
Phần trình bày trên mô tả một cách nhìn khái quát về mô hình, cũng như các phương pháp ước lượng SEMs. Một dạng SEMs thường được sử dụng trong nghiên cứu đó là ước lượng SEMs với dữ liệu bảng.




